| 6.2 |
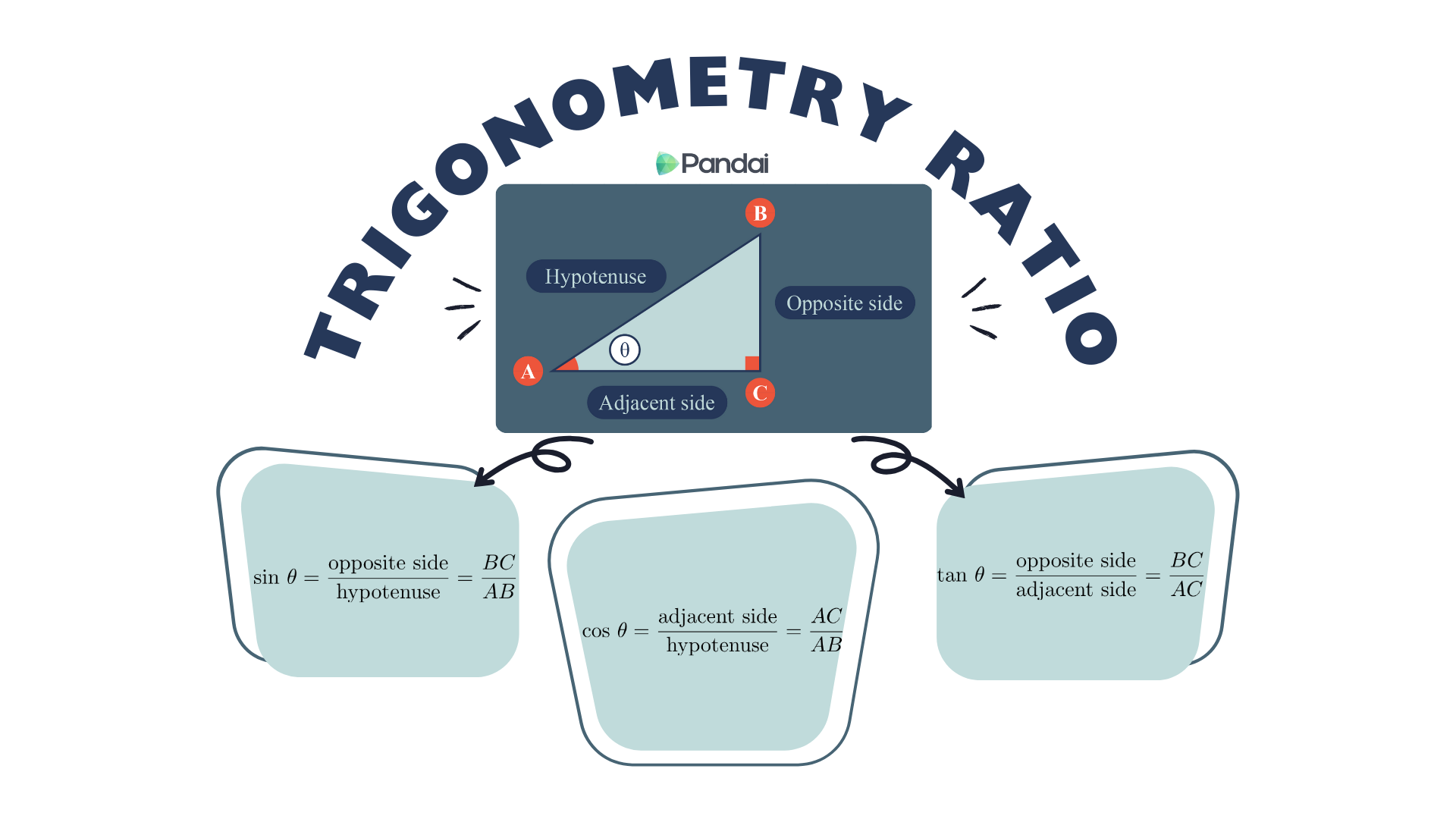
Trigonometric Ration of Any Angle |
|
| |
 |
| |
| Formula of Cosecant, Secant and Cotangent |
|
\(\text{cosec }\theta= \dfrac{1}{\text{sin }\theta}\)
|
|
\(\text{sec }\theta= \dfrac{1}{\text{cos }\theta}\)
|
|
\(\text{cot }\theta= \dfrac{1}{\text{tan }\theta}\)
|
|
| |
| Complementary Angles |
|
The angles \(A\) and \(B\) are complementary angles to each other if \(A+B=90^\circ\). Hence,
\(A=90^\circ-B\) and \(B=90^\circ-A\)
|
|
| |
| Formula of the Complementary Angles |
- \(\text{sin }\theta= \text{cos } (90^{\circ}-\theta)\)
- \(\text{cos }\theta= \text{sin } (90^{\circ}-\theta)\)
- \(\text{tan }\theta= \text{cot } (90^{\circ}-\theta)\)
- \(\text{sec }\theta= \text{cosec } (90^{\circ}-\theta)\)
- \(\text{cosec }\theta= \text{sec } (90^{\circ}-\theta)\)
- \(\text{cot }\theta= \text{tan } (90^{\circ}-\theta)\)
|
|
| |
| \(4\) Methods to Determine the Values of the Trigonometric Ratios for Any Angle |
| Method \(1\): Use a Calculator |
- The values of sine, cosine and tangent can be determined by using a calculator.
- The values for cosecant, secant and cotangent can be calculated by inversing the values of the trigonometric ratios of sine, cosine and tangent of that particular angle.
|
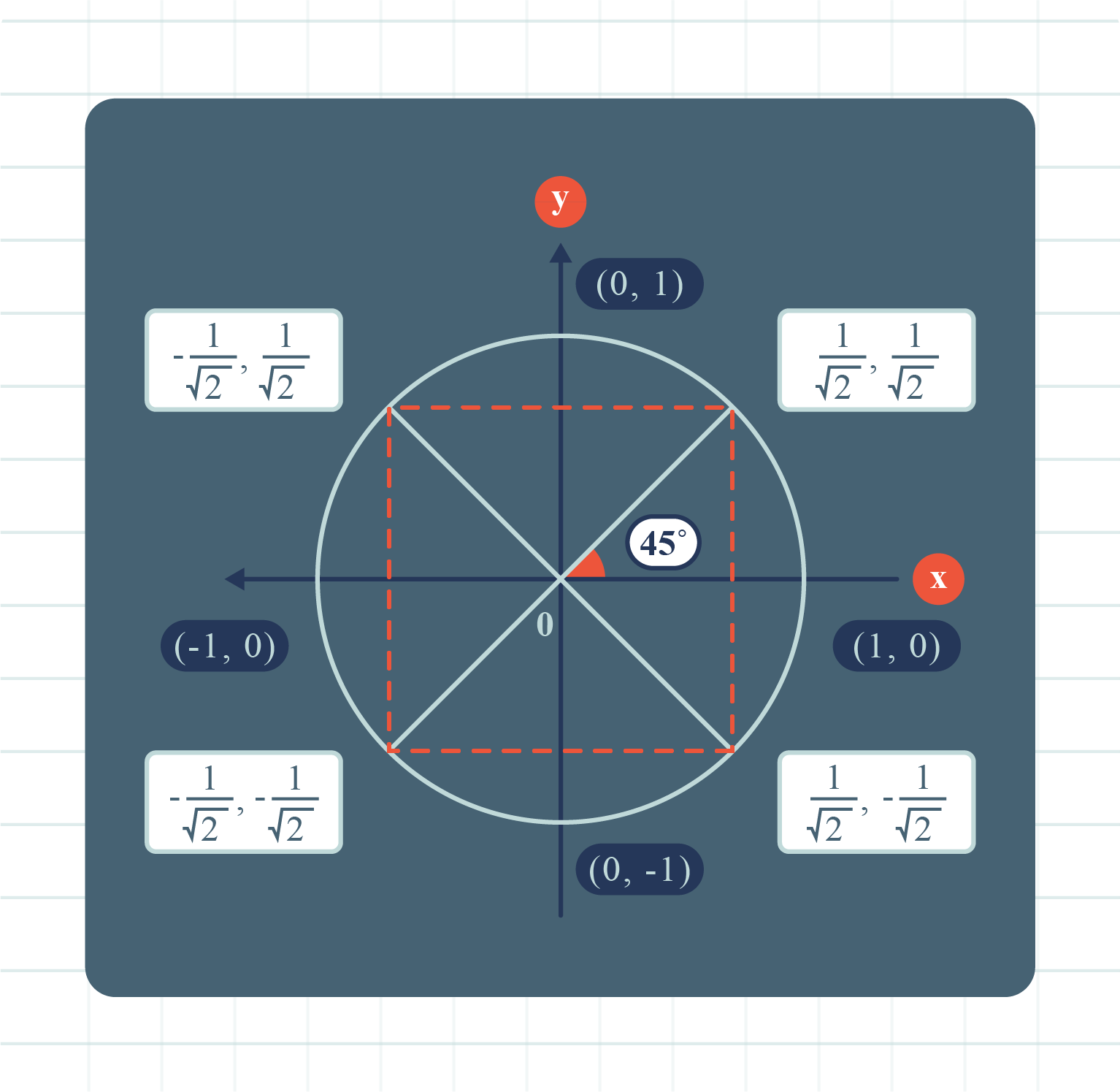
| Method \(2\): Use a Unit Circle |
|
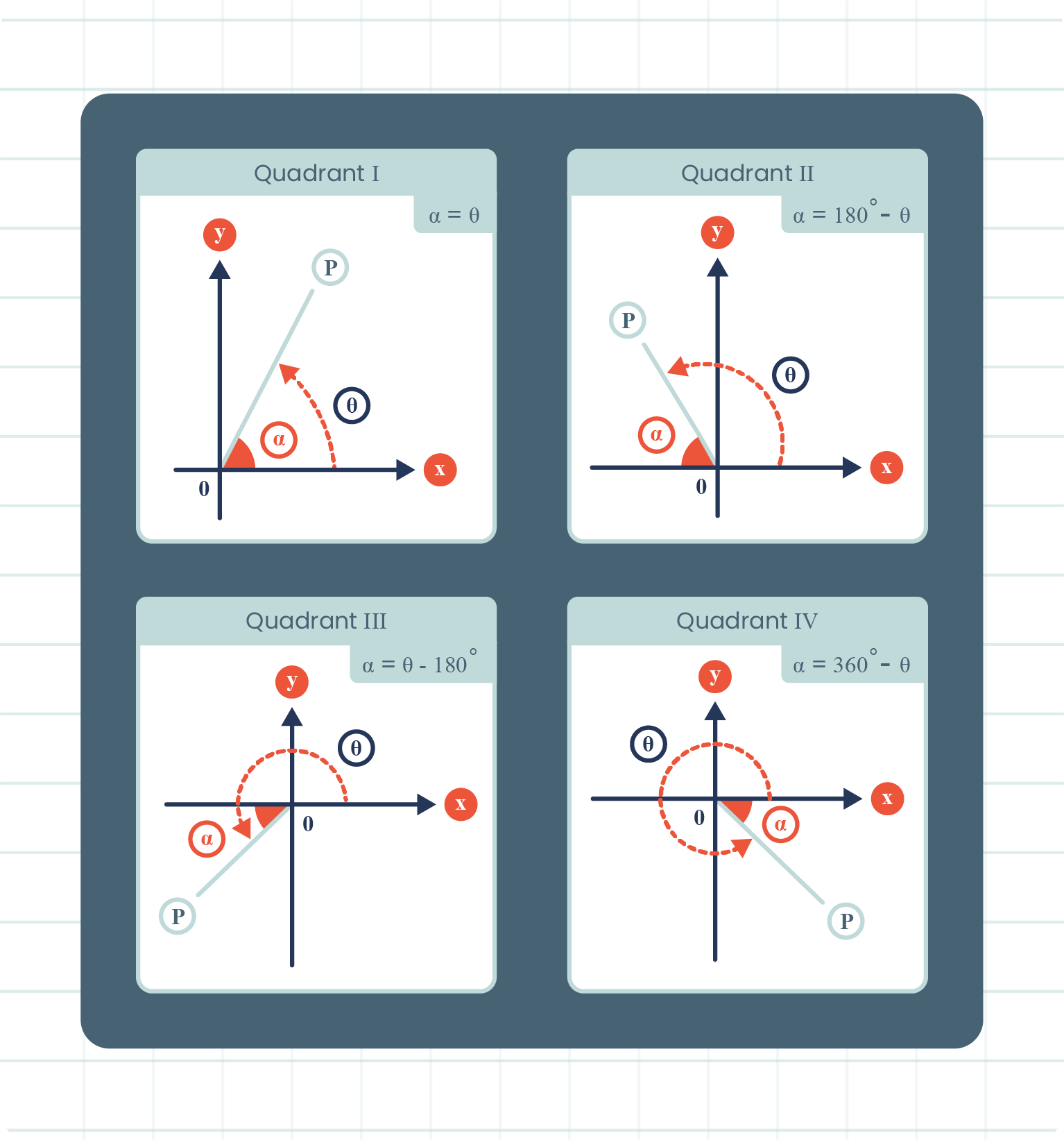
| Method \(3\): Use the Corresponding Trigonometric Ratio of the Reference Angle |
The diagram shows the reference angles, \(\alpha\) for the angles \( 0° \leqslant \theta \leqslant 360^{\circ}\) or \( 0° \leqslant \theta \leqslant 2\pi\).
|
| Method \(4\): Use a Right-angled Triangle |
The trigonometric ratios of special angles \(30^\circ\), \(45^\circ\) and \(60^\circ\) can be determined by using right-angled triangles.
| Angle / Ratio |
sin |
cos |
tan |
cosec |
sec |
cot |
| \(30^\circ\) |
\(\dfrac{\pi}{6}\) |
\(\dfrac{1}{2}\) |
\(\dfrac{\sqrt{3}}{2}\) |
\(\dfrac{1}{\sqrt{3}}\) |
\(2\) |
\(\dfrac{2}{\sqrt{3}}\) |
\(\sqrt{3}\) |
| \(45^\circ\) |
\(\dfrac{\pi}{4}\) |
\(\dfrac{1}{\sqrt{2}}\) |
\(\dfrac{1}{\sqrt{2}}\) |
\(1\) |
\(\sqrt{2}\) |
\(\sqrt{2}\) |
\(1\) |
| \(60^\circ\) |
\(\dfrac{\pi}{3}\) |
\(\dfrac{\sqrt{3}}{2}\) |
\(\dfrac{1}{2}\) |
\(\sqrt{3}\) |
\(\dfrac{2}{\sqrt{3}}\) |
\(2\) |
\(\dfrac{1}{\sqrt{3}}\) |
|
|
| |
| Example \(1\) |
| (a) |
Given that \(\text{sin } 77^{\circ} = 0.9744\) and \(\text{cos } 77^{\circ} = 0.225\). |
| |
Find the value of \(\text{cos }13^{\circ}\). |
| |
|
| (b) |
Given \(\text{cos }63^{\circ} = k\), where \(k \gt 0\). |
| |
Find the value of \(\text{cosec }27^{\circ}\) in terms of \(k\). |
|
|
(a)
\(\begin{aligned} \text{cos }\theta&= \text{sin } (90^{\circ}-\theta)\\ \text{cos }13^{\circ}&= \text{sin } (90^{\circ}-13^{\circ})\\ &= \text{sin }77^{\circ}\\ &= 0.9744. \end{aligned}\)
(b)
\(\begin{aligned} \text{cosec }\theta&= \text{sec } (90^{\circ}-\theta)\\ \text{cosec }27^{\circ}&= \text{sec } (90^{\circ}-27^{\circ})\\ &= \text{sec }63^{\circ}\\ &= \dfrac{1}{\text{cos }63^{\circ}}\\ &= \dfrac{1}{k}. \end{aligned}\)
|
|
| |
| Example \(2\) |
|
Use the unit circle and state the value of \(\text{cos }135^{\circ}\).
|
|
The coordinates that correspond to \(135^{\circ}\) are
\(\begin{pmatrix} -\dfrac{1}{\sqrt2}, \ \dfrac{1}{\sqrt2} \end{pmatrix}\) and \(\text{cos }135^{\circ} = x\text{-coordinate}\).
Hence, \(\text{cos }135^{\circ} = -\dfrac{1}{\sqrt2}\).
|
|
| |