Area of a sector of a circle

Back

Area of Sector of a Circle

1.3

Area of Sector of a Circle

$The image is an educational graphic explaining the area of a sector of a circle. It has three main sections: 1. The central section is titled ‘Area of Sector of a Circle’ in a dark blue bubble. 2. The top right section, labeled ‘Sector of a Circle,’ defines a sector as a region of a circle bounded by two radii and the arc between them. 3. The bottom right section, labeled ‘Area of a Sector,’ explains that the area of a sector is a fraction of the area of the entire circle. The graphic also includes the Pandai logo at the bottom left.$

Type of Sector

If a circle is divided into two sectors of different sizes, the smaller sector is known as the minor sector while the larger sector is known as the major sector.

Formula for Area of a Sector

Figure

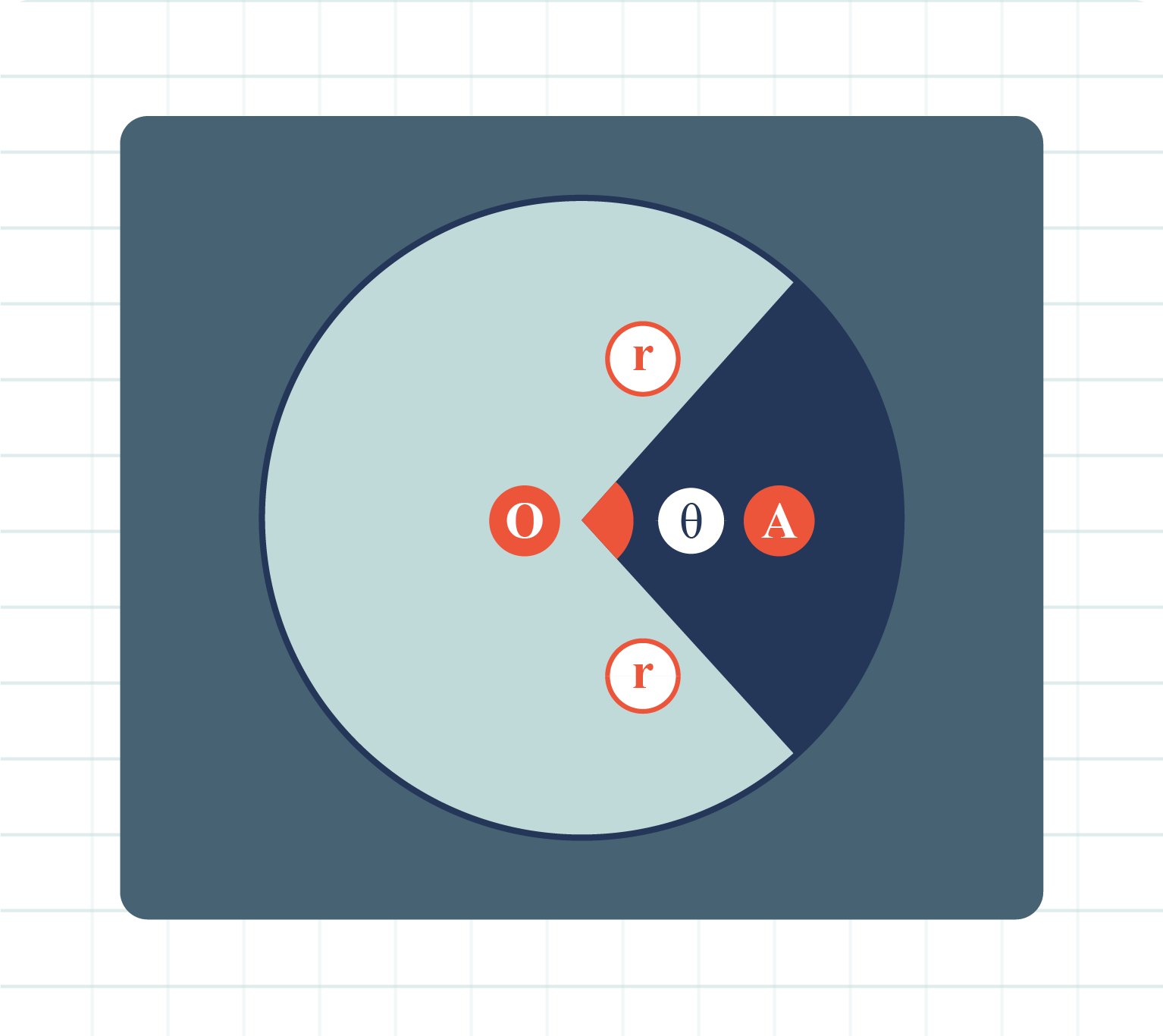
Diagram illustrating a circle with major and minor sector, highlighting radius, angle, and arc length concepts.

When Angle is in Radians

Based on the diagram above, area of sector can be write as:

$\text{Area}=\dfrac{1}{2}r^2\theta$

where $r$ is the radius and $\theta$ is the angle in radians.

When Angle is in Degrees

Another formula to calculate the area of a sector is given by:

$\text{Area}=\dfrac{\theta}{360^\circ}\times\pi r^2$

where $r$ is the radius and $\theta$ is the angle in degrees.

Area of a Segment

Figure

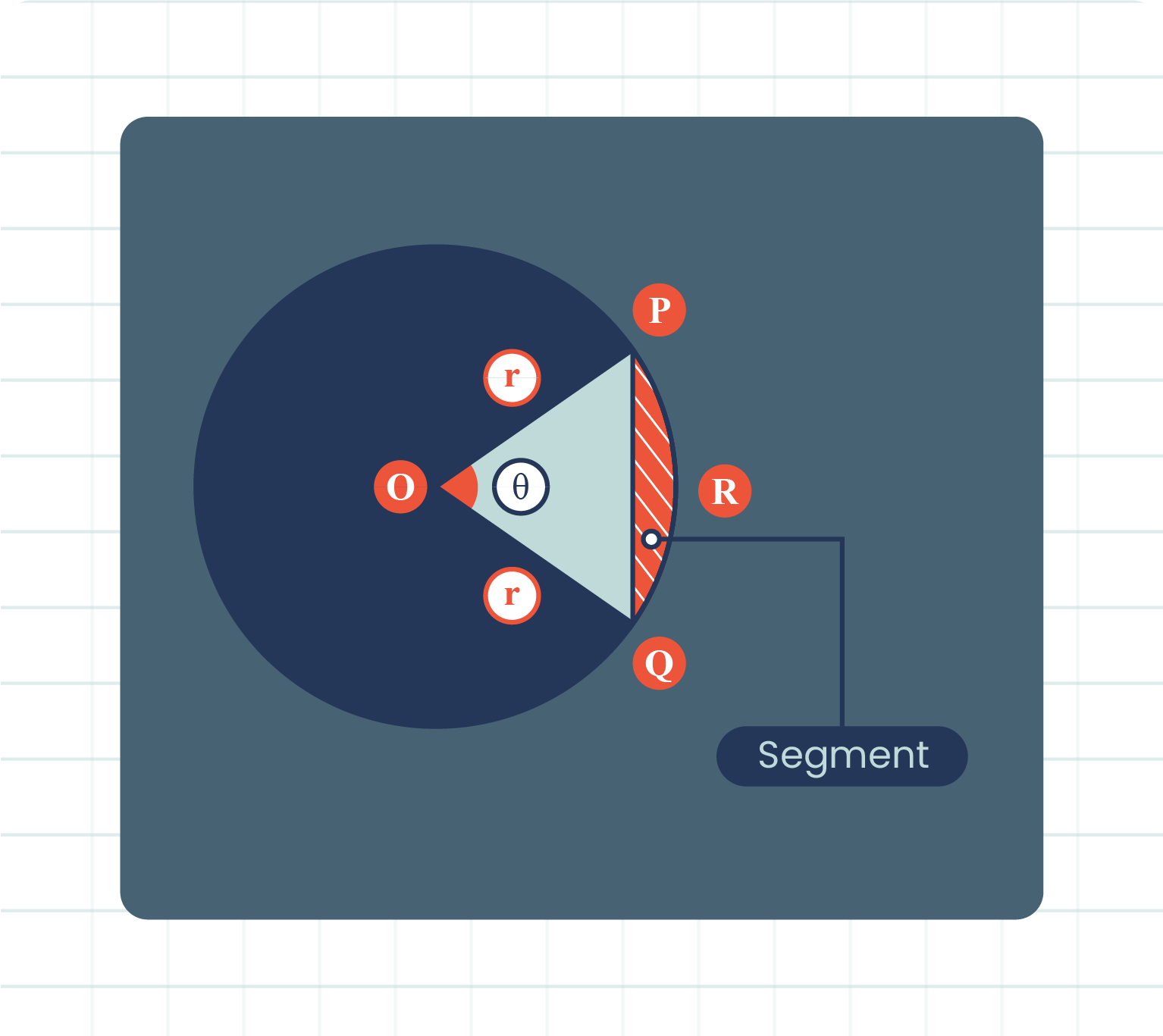
Diagram illustrating a segment, highlighting their geometric relationship in a circular context.

Formula for Area of Segment

Based on figure above, area of segment can be calculate by:

$= \text{Area of the sector } OPRQ - \text{Area of the isosceles }\triangle{OPQ} \ $

or can be calculated by using formula:

An image of a formula showing the area calculation for a segment, including both degrees and radians.

where $r$ is the radius of the sector and $\theta$ is the angle of the sector.

Example $1$

Question

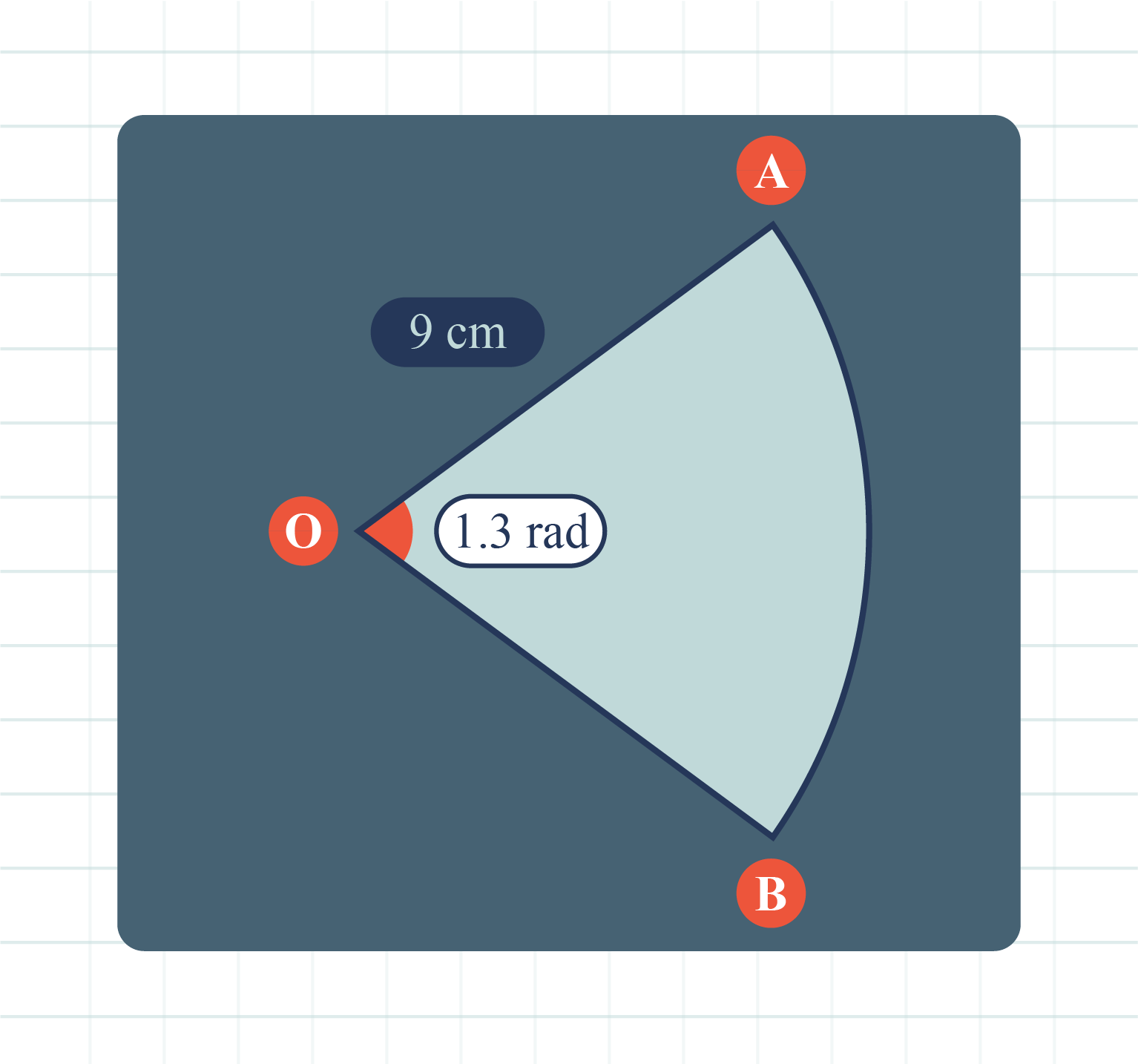
A diagram illustrating a circle within a circle, showcasing a minor sector with a radius of 9 cm and an angle of 1.3 radians.

Based on the diagram above, find the area of sector $AOB$.

Solution

Based on the figure, given,

$r=9$ cm,
$\theta=1.3\text{ rad}$.

Area of sector $AOB$:

$\begin{aligned} &=\dfrac{1}{2}r^2 \theta \\\\ &=\dfrac{1}{2}(9)^2(1.3) \\\\ &= 52.65 \text{ cm}^2. \end{aligned}$

Example $2$

Question

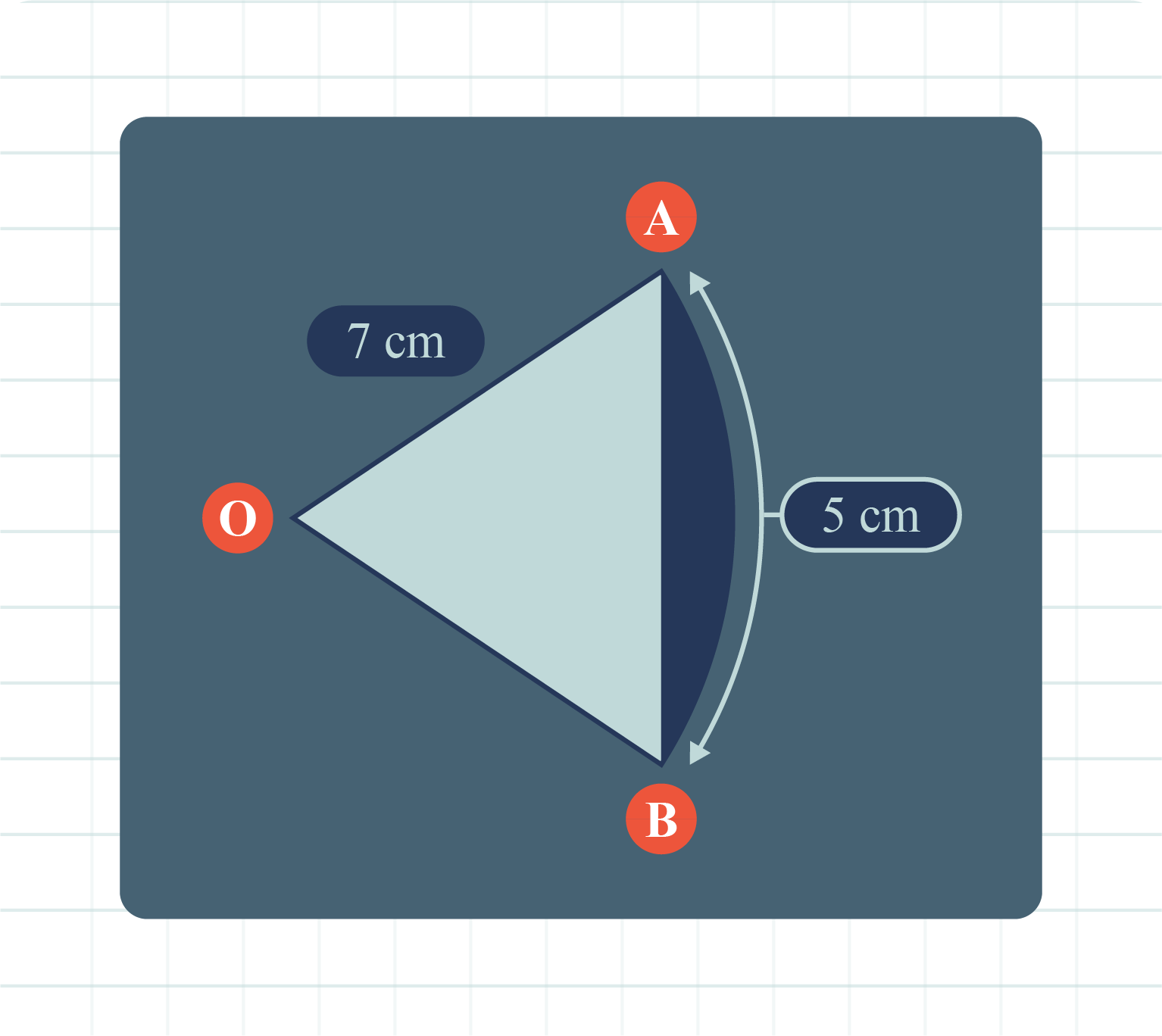
Diagram of a minor sector with a 7 cm radius, 5 cm arc length and shaded segment.

Diagram above shows a sector of a circle, with centre $O$ and a radius of $7$ cm.

The length of the arc $AB$ is $5$ cm.

Find the area of the shaded region.

[ Use $\pi=3.142$ ]

Solution

Find the value of $\theta$ by using arc length formula,

$\begin{aligned} s&=r\theta \\\\r\theta&=5 \\\\ 7\theta &=5 \\\\ \theta&=\dfrac{5}{7} \text{ rad}\\\\ \angle AOB&=\dfrac{5}{7}\times \dfrac{180}{3.\,142} \\\\ &=40.92^\circ. \end{aligned}$

Area of shaded region,

$\begin{aligned} &=\dfrac{1}{2}r^2(\theta-\sin \theta) \\\\ &=\dfrac{1}{2}(7)^2 \begin{pmatrix} \dfrac{5}{7}-\sin40.92^\circ \end{pmatrix} \\\\ &=\dfrac{1}{2}(49)(0.\,0593) \\\\ &=1.\, 4529 \text{ cm}^2.\end{aligned}$

Area of Sector of a Circle

Chapter : Circular Measure

Topic : Area of a sector of a circle

Related notes