| 2.1 |
Limit and Its Relation to Differentiation |
|
| |
 |
| |
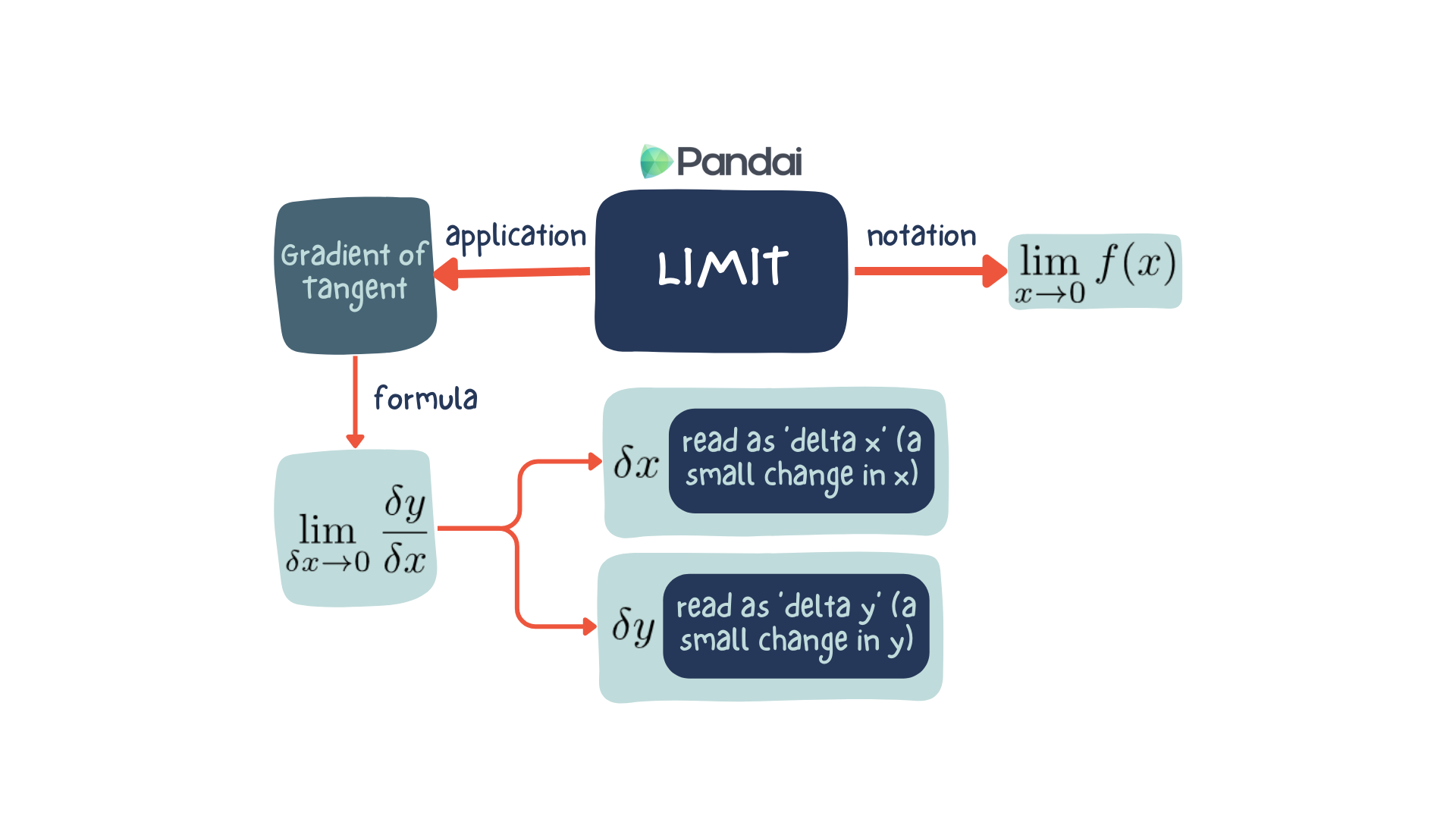
| Definition of Limit |
| When \(x\) approaches \(a\), where \(x\neq a\), the limit for \(f(x)\) is \(L\) can be written as \(\lim_{x \to a} f(x) = L\). |
|
| |
| Methods to Determine the Limit |
|
To find the limit value of a function \(f(x)\), we substitute \(x=a\) directly into the function \(f(x)\).
| Condition |
Method |
| \(f(a) \neq \dfrac{0}{0}\) |
The value of \(\lim_{x \to a} f(x)\) can be obtained, that is \(\lim_{x \to a} f(x) = f(a)\). |
| \(f(a) = \dfrac{0}{0}\) |
Determine \(\lim_{x \to a} f(x)\) by using the following methods:
- Factorisation,
- Rationalising the numerator or denominator of the function.
|
|
|
| |
| Definition of Tangent |
| A tangent to a curve at a point is a straight line that touches the curve at only that point. |
|
| |
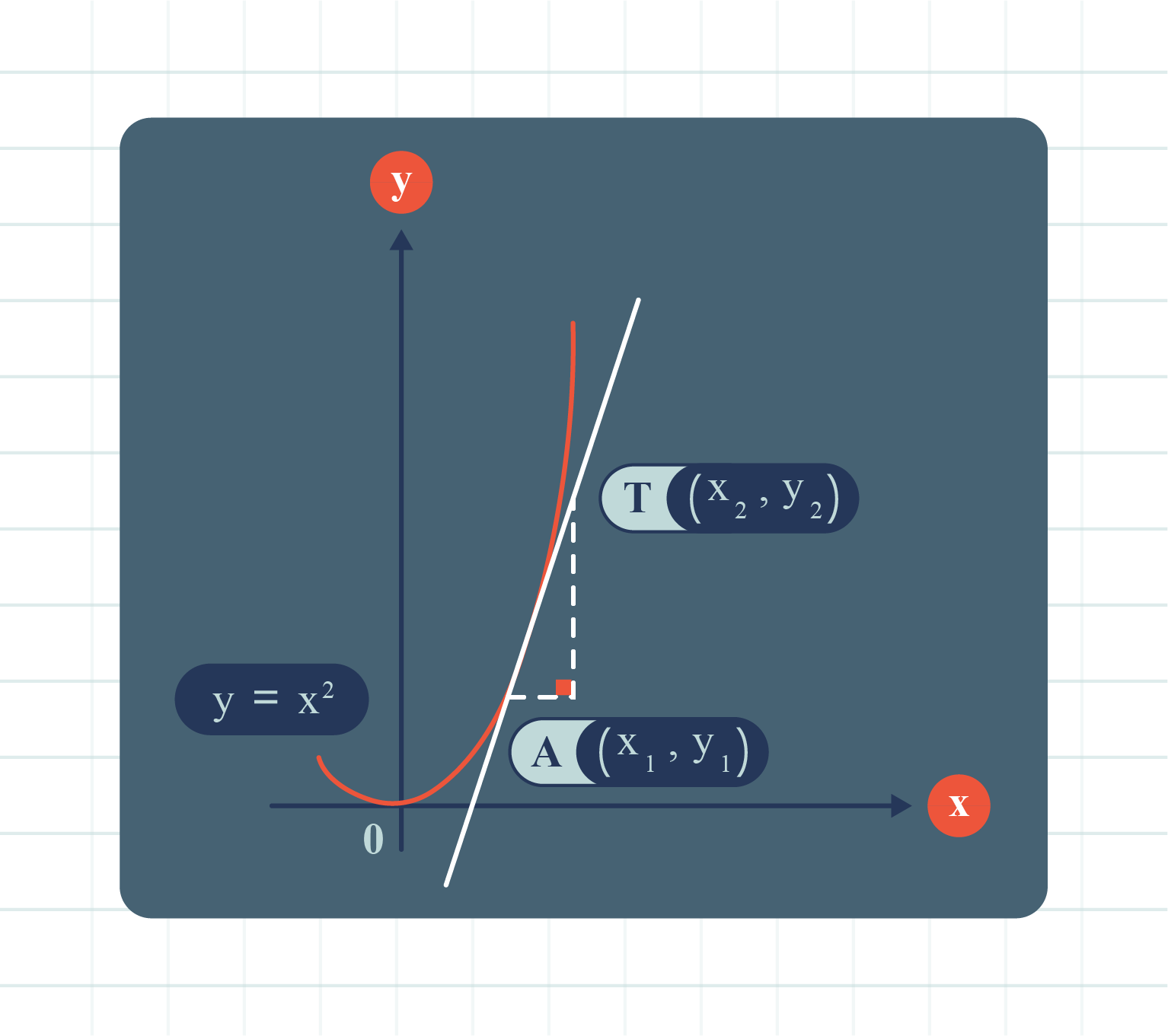
| Gradient of Tangent |
|
|
|
Based on the graph above, the line \(AT\) is a tangent to the curve \(y=x^2\) at the point \(A\):
\(\text{Gradient of tangent }AT = \dfrac{y_{2} - y_{1}}{x_{2} - x_{1}}\).
|
|
| |
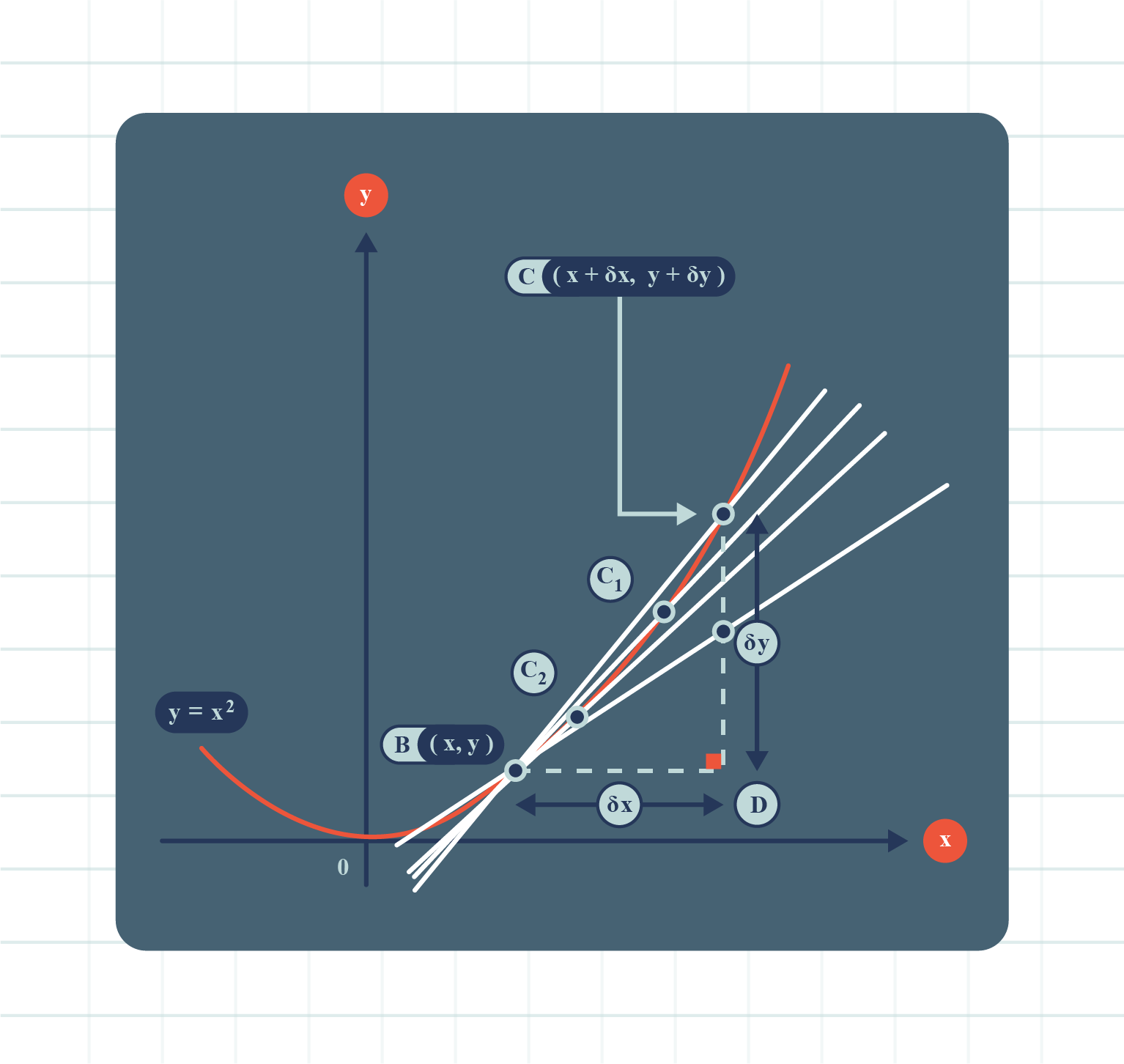
| Determining Gradients Using Limit |
|
|
- Based on the graph above, the gradient of the line \(BC\) can be calculated as follows:
\(\begin{aligned} &\text{Gradient of the line }BC \\&= \dfrac{CD}{BD}\\ &= \dfrac{(y- \delta y) -y}{(x+ \delta x) -x}\\ &= \dfrac{\delta y}{\delta x}. \end{aligned}\)
- For the curve \(y=f(x)\), the gradient function of the tangent at any point can be obtained using the following formula:
\(\begin{aligned} &\text{Gradient of the curve at }B\\ &= \text{Gradient of tangent }BT\\ &= \lim_{\delta x \to 0} \dfrac{\delta y}{\delta x}. \end{aligned}\)
- \( \lim_{\delta x \to 0} \dfrac{\delta y}{\delta x}\) is the first derivatives of the function and is written with the symbol \(\dfrac{dy}{dx}\).
- The gradient function \(\dfrac{dy}{dx}\) is known as differentiation using first principles.
- It can be use to find the gradient of a tangent of a curve \(y=f(x)\) at a point \((x, f(x))\),
\(\begin{aligned} \ \dfrac{dy}{dx} &= \lim_{\delta x \to 0} \dfrac{\delta y}{\delta x}\\\\ &= \lim_{\delta x \to 0} \dfrac{f(x+\delta x) - f(x)}{\delta x}. \end{aligned}\)
|
|
| |
| Example \(1\) |
|
Determine the limit value for each of the following functions:
(a) \(\lim_{x \to 4} \dfrac{3- \sqrt{x}}{x+2}\),
(b) \(\lim_{x \to 1} \dfrac{x^2- 1}{x-1}\).
|
|
(a)
Use direct substitution.
\(\begin{aligned} \lim_{x \to 4} \dfrac{3- \sqrt{x}}{x+2} &= \dfrac{3- \sqrt{4}}{4+2} \\\\ &= \dfrac{3-2}{4+2}\\\\ &= \dfrac{1}{6} .\end{aligned}\)
(b)
When \(x=1\), \(\lim_{x \to 1} \dfrac{x^2- 1}{x-1}\) is in the indeterminate form, \(\dfrac{0}{0}\).
Thus, we need to factorise and eliminate the common factor before we can use direct substitution.
\(\begin{aligned} \lim_{x \to 1} \dfrac{x^2- 1}{x-1} &= \lim_{x \to 1} \dfrac{(x+1)(x-1)}{x-1} \\\\ &= \lim_{x \to 1} \ (x+1)\\\\ &= 1+1\\\ &=2. \end{aligned}\)
|
|
| |
| Example \(2\) |
|
Find \(\dfrac{dy}{dx}\) by using first principle for each of the following functions \(y=f(x)\).
(a) \(y=3x\),
(b) \(y=3x^2\).
|
|
(a)
Given \(y=f(x)=3x\),
\(\begin{aligned} \delta y &= f(x+\delta x) - f(x)\\ &= 3(x+\delta x) - 3x\\ &= 3x + 3 \delta x-3x\\ &= 3 \delta x\\ \dfrac{\delta y}{\delta x}&= 3. \end{aligned}\)
Hence,
\(\begin{aligned} \dfrac{dy}{dx} &= \lim_{\delta x \to 0} \dfrac{\delta y}{\delta x}\\\\ &= \lim_{\delta x \to 0} 3\\\\ &=3. \end{aligned}\)
(b)
Given \(y=f(x)=3x^2\),
\(\begin{aligned} \delta y &= f(x+\delta x) - f(x)\\ &= 3(x+\delta x)^2 - 3x^2\\ &= 3[x^2 + 2x(\delta x) + (\delta x)^2] - 3x^2\\ &= 3x^2 + 6x(\delta x) + 3(\delta x)^2 - 3x^2\\ &=6x(\delta x) + 3(\delta x)^2\\ \dfrac{\delta y}{\delta x}&= 6x+3\delta x .\end{aligned}\)
Hence,
\(\begin{aligned} \dfrac{dy}{dx} &= \lim_{\delta x \to 0} \dfrac{\delta y}{\delta x}\\\\ &= \lim_{\delta x \to 0} (6x+3\delta x)\\\\ &=6x+3(0)\\ &= 6x. \end{aligned}\)
|
|
| |