|
|
| |
 |
| |
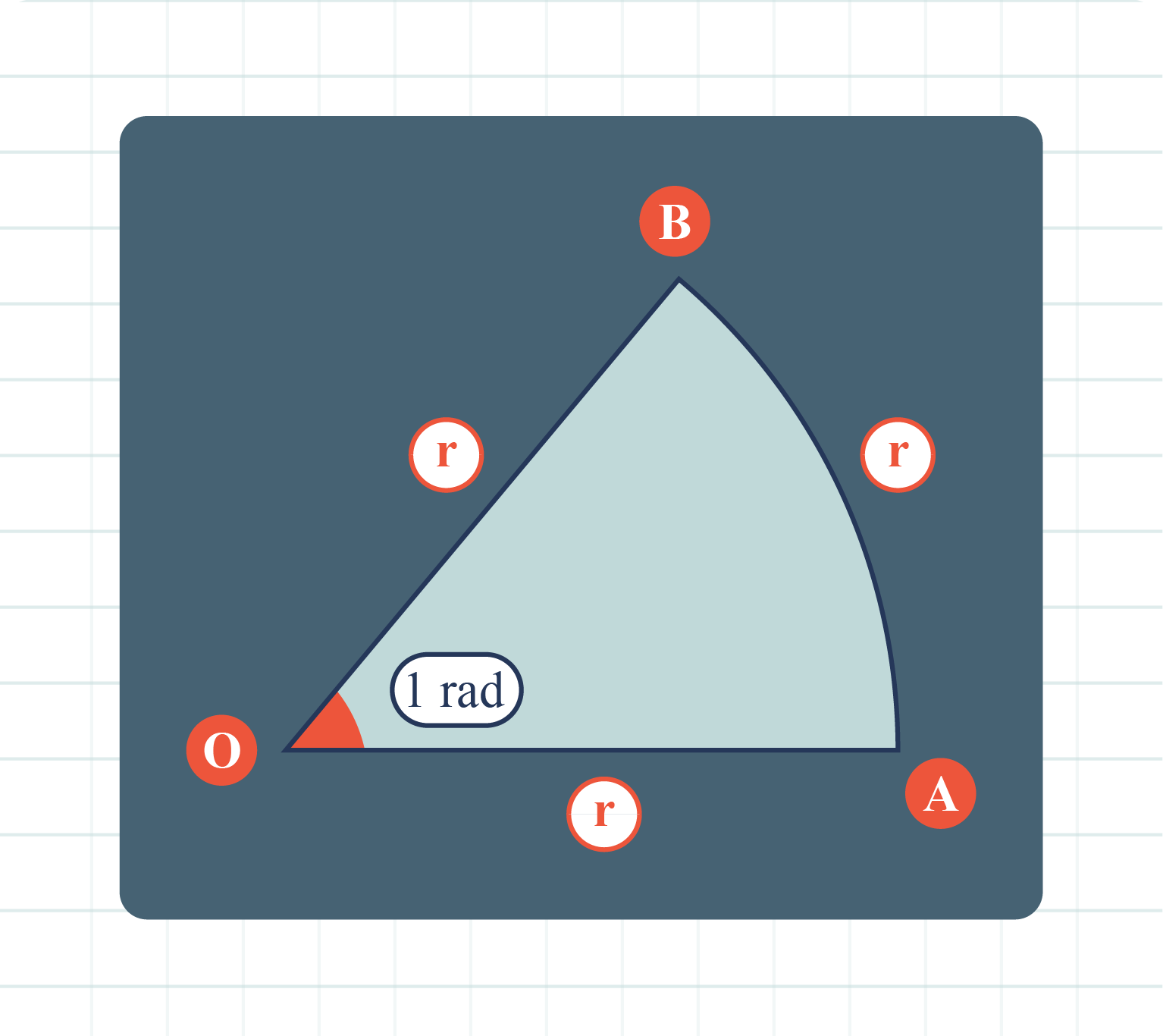
| Definition of One Radian |
|
The angle subtended at the centre of a circle is \(1\) radian if the length of the arc is equal to the radius of the circle.
|
|
|
|
| |
| Relationship with Degrees |
- \(1\text{ rad}=\dfrac{180^\circ}{\pi}\)
- \(360^\circ=2\pi \text{ rad}\)
|
|
| |
| Conversion Formula |
- To convert degrees to radians:
\(\text{radians}=\text{degrees}\times \dfrac{\pi}{180^\circ}\)
- To convert radians to degrees:
\(\text{degrees}=\text{radians}\times\dfrac{180^\circ}{\pi}\)
|
|
| |
| Example \(1\) |
|
Convert \(120^\circ\) to radians.
|
|
\(\begin{aligned} \text{radians}&=120^\circ\times\dfrac{\pi}{180^\circ} \\\\ &=\dfrac{2\pi}{3}\text{ rad} .\end{aligned}\)
|
|
| |
| Example \(2\) |
|
Convert \(\dfrac{\pi}{4}\text{ rad}\) to degrees.
|
|
\(\begin{aligned} \text{degrees}&=\dfrac{\pi}{4}\text{ rad}\times\dfrac{180^\circ}{\pi} \\\\ &=45^\circ. \end{aligned}\)
|
|
| |