| |
| 11.2 |
Venn Diagrams, Universal Sets, Complement of a Set and Subsets |
|
| |
| Universal set: |
| |
| Definition |
|
A set that consists of all the elements under discussion.
|
|
| |
- The symbol for universal set is \(\xi\).
|
| |
| Complementary set: |
| |
| Definition |
|
The elements in the universal set that are not the elements of the set.
|
|
| |
| Example |
|
Tthe following is the universal set and set \(P\).
\(\begin{aligned} \xi&=\{2, 3, 4, 5\} \\\\P&=\{2, 3, 5\}\end{aligned}\)
(i) State whether set \(P\) is a universal set.
(ii) Based on the universal set, determine the complement of set \(P\).
|
|
(i)
Set \(P\) is not a universal set as it does not contain element \(4\).
|
|
(ii)
The complement of set \(P\) is
\(P'=\{4\}\).
|
|
| |
| Represent the universal set and complement of a set by using Venn diagram: |
| |
- A set can be represented by a circle, an oval, a rectangle or a triangle.
- The universal set is commonly represented by a rectangle.
- A set can also be represented by an enclosed geometrical diagram which is known as Venn diagram.
|
| |
| Example |
|
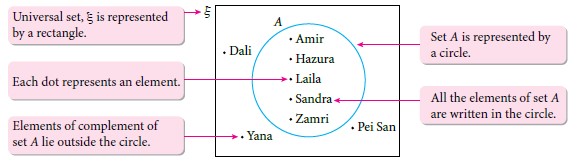
\(\begin{aligned} \xi&=\{\text{Amir, Hazura, Laila, Sandra,} \\&\quad\quad \text{Zamri, Dali, Pei San, Yana}\} \\\\A&=\{\text{Amir, Hazura, Laila} \\&\quad\quad \text{Sandra, Zamri}\}\\\\A'&=\{\text{Dali, Pei San, Yana}\} \end{aligned}\)
|
|
|
|
| |
| Subset of a set: |
| |
| Definition |
|
A set whereby all of its elements are the elements of another set.
|
|
| |
- The symbol for subset is \(\subset\).
- ‘Is not a subset of’ can be denoted using the symbol \(\cancel{\subset}\).
|
| |
| Example |
|
Given the following sets.
\(\begin{aligned} Q&=\{x,y\} \\\\R&=\{v,w,x,y, z\} \end{aligned}\)
Is set \(Q\) is the subset of set \(R\)?
|
|
Yes, set \(Q\) is the subset of set \(R\) because every element of \(Q\) is found in \(R\).
|
|
| |
- Empty set, \(\phi\) is a subset of any set.
- Set itself is a subset of any set.
- If a set contains \(n\) elements, then the possible number of subsets is \(2^n\).
|
| |
| Example |
|
List all the possible subsets for set \(\{k,l\}\).
|
|
We can see that the set contains \(2\) elements.
So, the possible number of subsets is
\(2^2=4\).
Thus, the possible subsets is
\(\phi,\{k\},\{l\},\{k,l\}\).
|
|
| |
| Represent subsets using Venn diagrams: |
| |
- For an infinite set, its elements need not be written.
|
| |
| Example |
|
Given that,
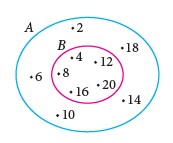
\(\begin{aligned} A&=\{2, 4, 6, 8, 10,12, 14, 16, 18, 20\}\\\\B&=\{4, 8, 12, 16, 20\} \end{aligned}\)
The relationship of \(B\subset A\) can be represented using the Venn diagram as shown below.
|
|
| |