Back

Linear Programming Model

7.1 Linear Programming Model
 
The image is an infographic titled 'Steps to Form a Linear Programming Model.' It features three main steps, each enclosed in a box with a corresponding number and description: 1. **Identify the decision variables**: Decision variables describe the decisions that need to be made and can be represented by x & y. 2. **Identify the objective functions**: An objective function is a function that needs to be maximized or minimized. 3. **Identify the constraints**: Present the existing constraints in the form of equations or linear inequalities, which use symbols like ≤, <, =, >, and/or ≥. Constraints must be in terms of decision variables. The infographic has a clean and structured design, using blue and white colors for clarity.
 
Forming a Mathematical Model for a Situation Based on Given Constraints and Representing the Model Graphically
Description

A mathematical model can be formulated by using the variables \(x\) and \(y\) with the constraints in each situation being \(\leq\), \(\ge\), \(\lt\) or \(\gt\).

  • The region above the straight line \(ax+by=c\) satisfies the inequalities \(ax+by\ge c\) and \(ax+by\gt c\), where \(b \gt 0\).
  • The region below the straight line \(ax+by=c\) satisfies the inequalities \(ax+by\le c\) and \(ax+by \lt c\), where \(b\gt 0\).
  • The region on the right side of the line \(ax=c\) satisfies the inequalities \(ax\ge c\) and \(ax \gt c\).
  • The region on the left side of the line \(ax=c\) satisfies the inequalities \(ax\le c\) and \(ax \lt c\).
Summary

If a mathematical model involves signs like:

  • \(\ge\) or \(\le\), then a solid line \((\overline{\hspace{1cm}})\) is used.
  • \(\lt\) or \(\gt\), then a dotted line \((\text{-} \text{ -} \text{ -} \text{ -}\text{ -})\) is used.
Objective Function

An objective function is written as:

\(k=ax+by\)
 
Example \(1\)
Question
(a) Write a mathematical model for the following situation:
  The perimeter of the rectangular photo frame must not be more than \(180\) cm.
   
(b) Present the inequalities \(x-2y \geqslant -4\) graphically.
Solution (a)

Supposed \(x\) and \(y\) are the width and length of the rectangular photo frame.

Then, \(2x+2y \text{ < }180\).
Solution (b)

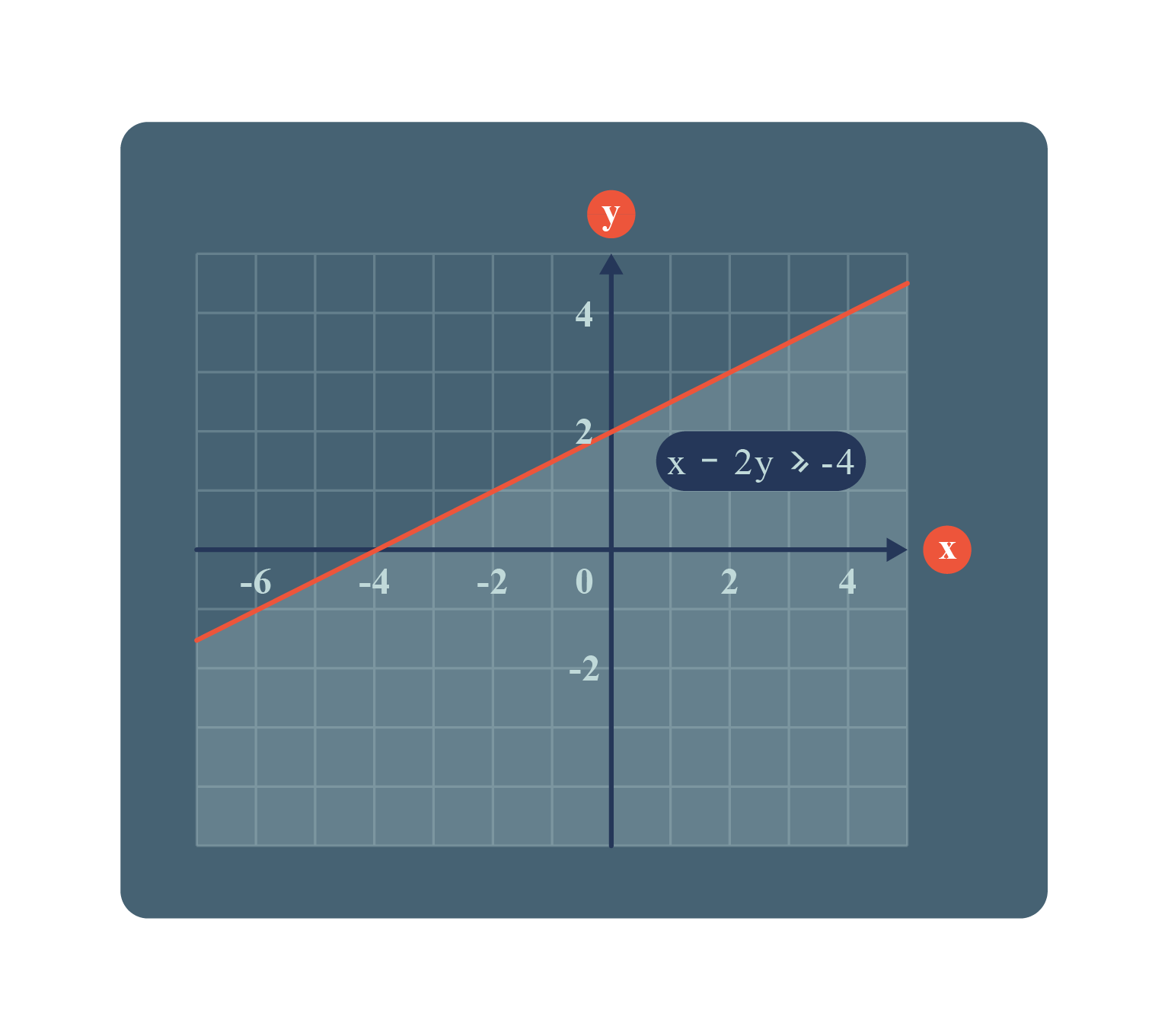
Given \(x-2y \geqslant -4\).

Since \(b=-2 \ (\text{< }0)\).

Hence, the region lies below the line \(x-2y=-4\).

1. A graph displaying a line with a distinct point marked on it, illustrating a specific data value or trend.
 
Example \(2\)
Question

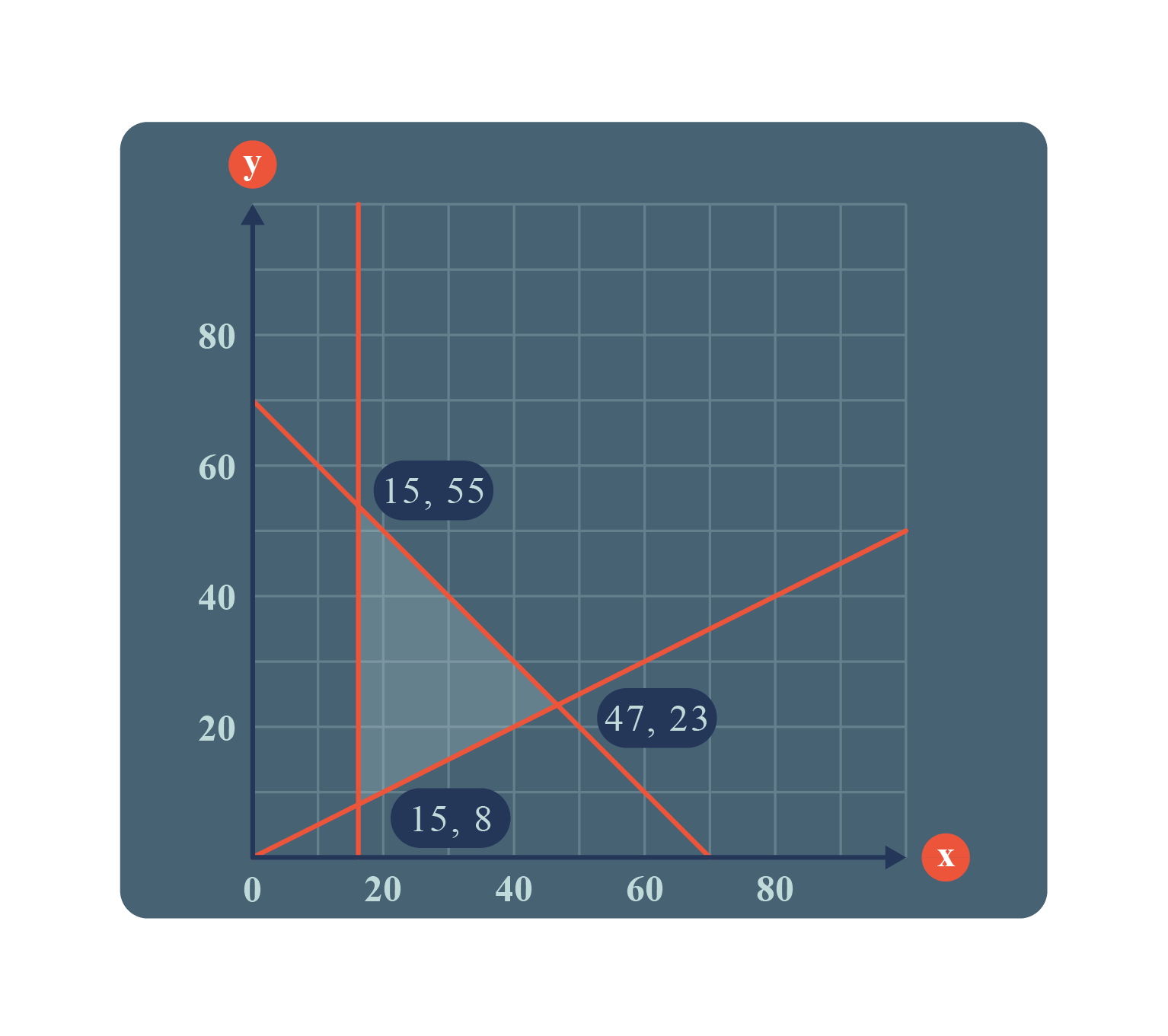
Graph illustrating product pricing trends, showcasing a linear programming model for analysis and decision-making.

The diagram above shows the shaded region that satisfies a few constraints of a situation.

Given \(k = x+2y\), find 

(a) the maximum value of \(k\),
(b) the minimum value of \(k\).
Solution
(a) Substitute the maximum point for the shaded region, which is \((15,55)\) into \(k = x+2y\).
  \(\begin{aligned} k&=15+2(55)\\ &=125. \end{aligned}\)
  Therefore, the maximum value of \(k\) is \(125\).
   
(b) Substitute the minimum point for the shaded region, which is \((15,8)\) into \(k = x+2y\).
  \(\begin{aligned} k&=15+2(8)\\ &=31. \end{aligned}\)
  Therefore, the minimum value of \(k\) is \(31\).
 
The views expressed in the notes here are those of the contributor and don’t necessarily represent the views of Pandai.
Chapter : Linear Programming
Topic : Linear Programming Model
Form 5 Additional Mathematics
Related notes

Report this note
MY
EN