| |
Definition |
|
| |
|
|
| |
The transfer of all points on a plane in the same direction and through the same distance.
|
|
|
|
|
| |
|
|
|
|
| Representation of translation in the form of vector: |
|
|
| |
|
|
|
|
- Vector of translation is a movement that has direction and magnitude and is determined based on the value and direction of a vector.
|
|
|
| |
|
|
|
|
| Translation can be described using two methods, |
|
|
| |
|
|
|
|
|
(i)
|
|
The direction of movement: to the right, left, upwards or downwards
|
|
|
| |
|
|
|
| |
The direction of distance: number of units
|
|
|
| |
|
|
|
|
|
(ii)
|
|
Written in a vector form \(\dbinom{a}{b}\)
|
|
|
| |
|
|
|
|
| Image and object under a translation: |
|
|
| |
|
|
|
|
| Example |
|
|
| |
|
|
|
|
|
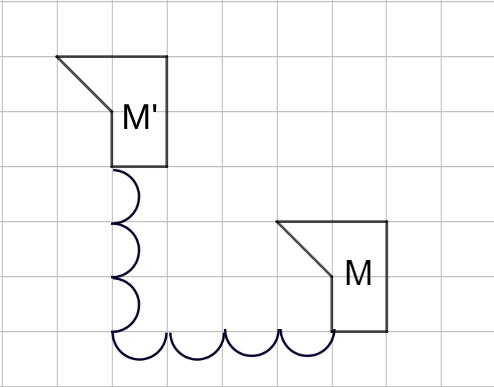
|
|
|
| |
|
|
- \(M'\) is the image of object \(M\).
- The translation is \(\dbinom{-4}{3}\).
|
|
|
| |
|
|
|
|
|
Determining the coordinate of the image when coordinate of the object is given:
|
| |
|
|
|
|
- To locate the image with translation \(\dbinom{a}{b}\), the coordinate of object \((x,y)\) will be mapped to image \((x+a, y+b)=(x',y')\).
|
|
|
| |
|
|
|
|
|
Two alternative methods are:
|
|
|
- \(\dbinom{a}{b} + \dbinom{x}{y} = \dbinom{a+x}{b +y}\)
|
|
|
| |
|
|
- \(\dbinom{a}{b} - \dbinom{x}{y} = \dbinom{a-x}{b -y}\)
|
|
|
| |
|
|
|
|
|
Determining the coordinate of the object when the coordinate of the image is given:
|
| |
|
|
|
|
- To locate an object with translation \(\dbinom{a}{b}\), the coordinate of image \((x',y')\) will be mapped to object \((x'-a, y'-b)=(x,y)\).
|
|
|
| |
|
|
|
|
|
The alternative method is:
|
|
|
| |
|
|
- \(\dbinom{x}{y} = \dbinom{x'}{y'} - \dbinom{a}{b} \)
|
|
|
| |
|
|
|
|
|
Defining vector translation when the position of image and object is given:
|
|
|
| |
|
|
|
|
|
Given object \((x,y)\) and the image \((x',y')\).
\(\text{Vector Translation} = \dbinom{x' -x}{y' -y}\)
|
|
|