| |
|
|
| |
| What is similarity? |
| |
| Two objects are similar if they have the same shape, or one has the same shape as the mirror image of the other. |
| |
| For example, all circles are similar to each other, all squares are similar to each other, and all equilateral triangles are similar to each other. |
| |
| Note: If all the corresponding sides of a pair of triangles are proportional, then all the corresponding angles are equal and vice versa. |
| |
| Note: If two angles of a triangle have measures equal to the measures of two angles of another triangle, then the triangles are similar. |
| |
|
|
| |
| Example 2 |
| |
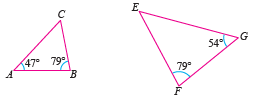
| Determine whether the pair of the following geometric objects are similar. |
| |
 |
| |
| Solution: |
| |
| \[\begin{aligned} \angle C&=180^{\circ}-47^{\circ}-79^{\circ}\\ &=54^{\circ}\\ &=\angle G\\ \angle B&=\angle F=79^{\circ}\\ \angle A&=\angle E=47^{\circ}. \end{aligned}\]
Therefore, triangle \(ABC \) and triangle \(EFG\) are similar.
|
| |
|
|
| |
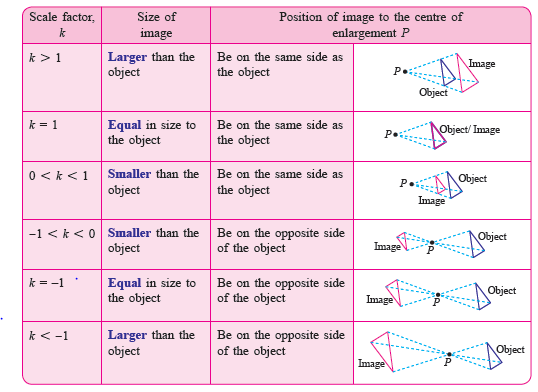
| Enlargement definition |
| |
| Enlargement is a transformation in which all the points of an object move from a fixed point with a constant ratio. The fixed point is known as the centre of enlargement and the constant ratio is known as the scale factor. |
| |
|
|
| |
| The scale factor \(k\), of an enlargement can be determined as follows. |
| |
| \[\begin{aligned} k&=\frac{\text{D.O.P of image from $P$}}{\text{D.O.P. of object from $P$}}\\ \\&\text{where}\\ &\text{D.O.P. is distance of point.}\end{aligned}\] or \[\begin{aligned} k=\frac{\text{length of side of image}}{\text{length of side of object}} \end{aligned}\] |
| |
 |
| |
|
|
| |
| Example 3 |
| |
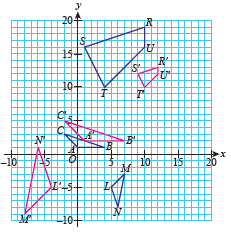
| The diagram below shows three objects and their images under the transformation of enlargement. Describe the enlargement by determining the scale factor and the centre of enlargement for the following: |
(a) object \(ABC \)
(b) object \(RSTU\)
(c) object \(LMN\) |
| |
 |
| |
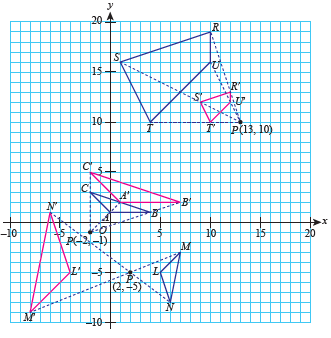
| Solution: |
| |
 |
| |
| a)\[\begin{aligned} &\text{Scale factor}\\&=\frac{A^\prime B^\prime}{AB}\\ &=\frac{6}{4}\\ &=\frac{3}{2}. \end{aligned}\]
\(A'B'C'\) is the image of \(ABC \) under an enlargement at centre \((-2,-1)\) with a scale factor of \(\dfrac{3}{2}\).
|
| |
| b)\[\begin{aligned} &\text{Scale factor}\\&=\frac{U^\prime R^\prime}{UR}\\ &=\frac{1}{3}. \end{aligned}\]
\(R'S'T'U'\) is the image of \(RSTU\) under an enlargement at centre \((13,10)\) with a scale factor of \(\dfrac{1}{3}\).
|
| |
c)
\[\begin{aligned} &\text{Scale factor}\\&=\frac{\text{distance of $L^\prime$ from }P}{\text{distance of $L$ from }P}\\ &=-\frac{6}{3}\\ &=-2.\end{aligned}\]Note: \(P\) is centre of enlargement.
\(L'M'N'\) is the image of \(LMN\) under an enlargement at centre \((2,-5)\) with a scale factor of \(-2\).
|
| |
|
|
| |
| Area of the image of an enlargement formula |
| |
| \(\text{Area of an image} \\= k^2\times\text{Area of the object}\) |
| |
| where \(k\) is the scale factor. |
| |
|
|
| |
| Example 4 |
| |
| Given an area of object and image are \(\text{5 cm}^2\) and \(\text{45 cm}^2\) respectively. Calculate the scale factor, \(k\). |
| |
| Solution: |
| |
| \[\begin{aligned} k&=\sqrt{\frac{\text{Area of the image}}{\text{Area of the object}}}\\ &=\sqrt{\frac{45}{5}}\\ &=\sqrt{9}\\ &=3. \end{aligned}\] |
| |
|
|
| |